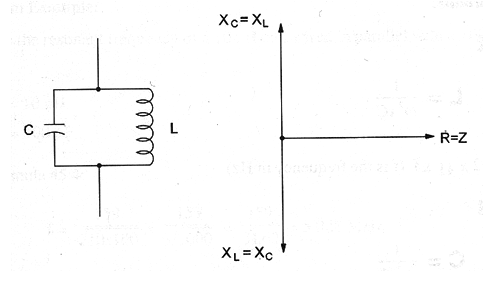
The frequency in which the capacitive reactance of an LC circuit becomes equal to the inductive reactance is termed “resonant frequency” and both for parallel and series circuits can be calculated by the following formula:
Formula 1
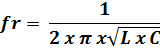
Where:
fr is the ressonant frequency in hertz (Hz)
L is the inductance in henrys (H)
C is the capacitancein farads (F)
π = 3,1416
Note: you can use multiples and submultiples of the units for capacitance and inductance finding results in multiples of hertz. If the inductance is in henry and the capacitance in farad the frequency is found in hertz. If the inductance is in microhenry and the capacitance in microfarad the frequency will be found in megahertz (MHz).
Derivated Formulas:
Formula 2
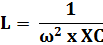
Where:
ω = 2 x π x f? = 2 x ? x f (f is the frequency in hertz)
Formula 3

Formula 4
When capacitances are in PF, inductance in µH and frequency in MHz, the following formula can be used:
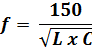
Formula 5
When the capacitance is in PF, inductance in mH, frequency is in kHz and the following formula can be used.
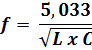
Importante Properties:
In the ideal series circuit at the resonant frequency the impedance is infinite.
In the ideal parallel circuit at the resonant frequency the impedance is zero.
Application Example:
Determine the resonant frequency of a 10 µH coil wired in parallel with a 100 pF capacitor.
Data:
L = 10 µH
C = 100 pF
Applying formula 4 (capacitances in pF and inductances in µH) we Will found the result in MHz.
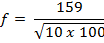
f = 159 / 31,62 = 5,028 MHz




