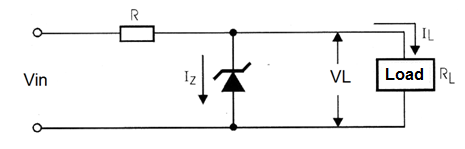
The following formulas are used in calculations related to a zener voltage regulator circuit as the one shown in figure bellow.
Formulas 1
Maximum current through a zener diode:
Iz(max) = [ Vin(max) – (VL + R x IL) / R ]
Where:
z(max) is the maximum current through the zener in amperes (A)
Iz(min) is the minimum current through the zener in amperes (A)
Vin(min) is the minimum input voltage in volts (V)
Vin(max) is the maximum input voltage in volts (V)
VL is the output voltage or load voltage in volts (V)
IL is the output current in amperes (A)
R is the resistance in ohms (Ω)
Formulas 2
The next formulas are used to calculate the range of values of R.
R(min) = [ Vin(max) – VL ] / [ Iz(max) + IL ]
R(max) = [ Vin(min) – VL ] / [ Iz(min) + IL ]
Where:
R(min) is the minimum value of R in ohm (Ω)
R(max) is the maximum value of R in ohm (Ω)
Vin(max) is the maximum input voltage in volts (V)
Vn(min) is the minimum input voltage in volts (V)
Iz(min) is the minimum zener current in amperes (A)
Iz(max) is the maximum zener current in amperes (A)
VL is the voltage across the load in volts (V)
IL is the load current in volts (V)
Formula 3
Maximum zener current:
Iz(max) = P(max) / Vz
Where:
Iz(max) is the maximum current in the zener diode in amperes (A)
P(max) is the maximum zener's power dissipation in watts (W)
Vz is the zener voltage in volts (V)
Derivated formula:
Formula 4
Maximum zener dissipation:
P(max) = Vz x Iz(max)
Where:
P(max) is the maximum power dissipated by the zener in watts (W)
Vz is the zener voltage
Iz(max) is the maximum current through the zener in amperes (A)
Application example:
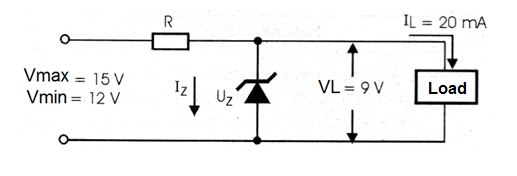
A 20 mA load must be powered from a 9 V regulated supply. The input voltage to the regulator circuit can change its value between 12 and 15 volts and the current through the zener must be kept between 10 and 50 mA. Calculate the value and dissipation of R.
Data:
IL = 20 mA
VL = 9 V
Vin(max) = 15 V
Vin(min) = 12 V
Iz(max) = 50 mA = 0.05 A
Iz(min) = 10 mA = 0.01 A
a) Calculating R(min) and R(max) - formula 2:
R(min) = (15- 9) / (0.05 – 0.02) = 6 / 0.03 = 200 Ω
R(max) = (12 – 9) / (0.02 – 0.01) = 3 / 0.01 = 300 Ω
We can adopt 220 Ω as it is a standard value for resistor and is in the calculated range.
b) Determining the dissipated power using formula 4:
P(max) = 0.05 x 9 = 0.45 Watt
A 1 W zener is the recommended to the application.




